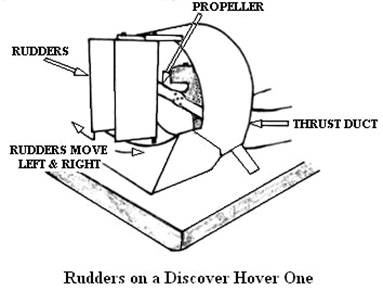
Figure 13-1: Rudders on a Discover Hover One
| NAME | DATE |
When driving a car, the friction of the rubber tires on the road allows almost instant change in direction when the steering wheel is turned. Piloting a hovercraft, however, is like driving a wet bar of soap, since with hovercraft you slide over most surfaces with little friction. Because ground contact friction is limited, hovercraft are easily affected by wind and surface slope. To maintain directional control of a conventional light hovercraft, two main techniques are employed. The first technique is kinesthetic steering. This occurs when the pilot leans in the direction he or she wants the hovercraft to turn. This increases the drag between the skirt and the ground on that side, causing it to move more slowly than the other side. This causes the hovercraft to turn. Cushion pressure acting on the bottom of the hovercraft hull also facilitates the turn. The second technique uses the rudders of the hovercraft to redirect the thrust air, changing the direction of the air. Remember that momentum is a vector quantity consisting of the product of the mass and the velocity, and that it is conserved in a system where the outside influences are very small compared to the changes within the system. In this case, the total momentum of the hovercraft and of the air must remain constant, so when the hovercraft rudders exert a force on the air to change its direction, the air exerts an equal but opposite force on the rudders according to Newton's Third Law of Motion. This causes a torque on the hovercraft through its approximate center of mass, turning it to face another direction. The table below summarizes quantities in linear and angular motion.
| Linear | Angular | Relation | ||
|---|---|---|---|---|
| Quantity | Unit | Quantity | Unit | |
| Mass (m) | kilogram [slug] (kg [slug]) | Moment of inertia (I) | kilogram meter2 [slug foot2] (kg-m2 [slug-ft2]) | I = m r2 (*) |
| Position (x) | meter [foot] (m [ft]) | Angular position (θ) | radian (rad) | θ = x / (2 × π) |
| Velocity (v) | meter [foot] per second (m/s [ft/s]) | Angular velocity (ω) | radian per second (rad/s) | ω = v × r &omega = Δθ / t |
| Acceleration (a) | meter [foot] per second per second (m/s2 [ft/s2]) | Angular acceleration (α) | radian per second per second (rad/s2) | α = a × r α = Δω / t |
| Momentum (p) | kilogram meter [slug foot] per second (kg-m/s [slug-ft/s]) | Angular momentum (L) | kilogram meter2 [slug foot2] / second (kg-m2/s [slug-ft2/s]) | L = p × r L = I × ω |
| Force (F) | newton [pound] (N [lb]) | Torque (τ) | newton meter [foot pound] (N-m [ft-lb]) | τ = F × r F = I × α |
| *The moment of inertia given is for a single point. The moment of inertia of an object depends on its shape, its mass, and the distribution of the mass. Also, each axis of rotation has a different moment of inertia. | ||||
Table 12-1: Quantities in Linear and Angular Motion

Figure 13-1: Rudders on a Discover Hover One
Image ©2005 DiscoverHover
Example
1: Solution: Air Volume = Volume Flow Rate × Time Now that we know the mass, by using the velocity we can find the momentum of the air when the hovercraft is moving straight. Momentum = Mass × Velocity Since momentum is a vector quantity, we note that the momentum we just found is all in the direction straight behind the hovercraft. If we turn the air, some of the momentum will still be straight behind it, but some will be perpendicular to it, either straight to the left or to the right. We find the amounts of each by looking at the angle by which the air is deflected, then we use basic trigonometry to find out how it influences the momentum. Since the thrust system is still running at the same speed, the total airflow is not any different, so we know that the two components of the new momentum have to combine to be the same magnitude as the original.
Image ©2005 DiscoverHover The component parallel to the hovercraft affects only how fast the hovercraft travels; it does not affect how fast it turns. It will be less than it was when the rudders were straight, so the linear acceleration of the hovercraft will be less than it was before. What interests us now is the perpendicular component, which will tell us how the hovercraft moves. Perpendicular Momentum = Total Momentum × sin(Angle of deflection) This is the horizontal momentum of the air, so it is also the exact opposite of the horizontal momentum on the rudders of the hovercraft. Since the rudders are at the end of the hovercraft rather than in the middle, their change in momentum does not make the hovercraft simply slide sideways; instead, it rotates around its center of mass. To find out how fast the hovercraft turns, we multiply the hovercraft’s momentum by the distance between the rudders and the center of mass (since there is no fixed pivot point, the craft rotates around that point). This gives us the angular momentum. If we divide this number by the moment of inertia of the hovercraft around its center of mass, we get the angular velocity. To find the amount the hovercraft turns, we multiply the angular velocity by the time. Angular Momentum = Linear Momentum × Radius Radians are handy units for calculations, but it is often easier to understand angles in degrees, so we can convert from radians to degrees by multiplying the angle in radians with the number 180/π 1.338 radians × 180/π = 76.7° The hovercraft would rotate 76.7°. |
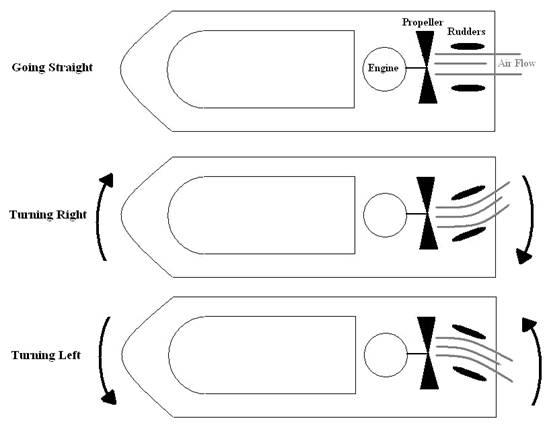
Figure 13-3: Turning of a Hovercraft
Image ©2005 DiscoverHover
You have changed the direction the hovercraft is facing, but the inertia of the hovercraft keeps it traveling in the original direction. Remember Newton’s First Law of Motion? We need a force to change the direction in which the hovercraft is moving. Now that you’re moving nearly sideways, you have a convenient force to do just that – the thrust system of your hovercraft! This is where the other component of the new momentum comes in. It’s really the same principle as the thrust in a straight line, just that now the thrust is not in line with the motion. When a car turns on the road, the tires on the ground experience a lot of friction, which keeps them from moving in a direction other than the direction they are facing. This is why you can steer a car and it will follow the course of the wheels. If the car is driving on ice, however, the coefficient of friction is much smaller, so there is very little friction to bind the car to its course. The same thing happens on a hovercraft, because no component touches the ground with enough force to “grip” the ground. Instead, the hovercraft must provide the force that would have come from friction by pointing the hovercraft into the turn. When this happens, a component of the thrust force is directed toward the center of the turn. A force toward the center of a turn, whether it is caused by the friction from a car's tires, a string keeping a ball from flying off, gravity between the earth and the sun, or the thrust from a turning hovercraft, is called a centripetal force. As you might expect, the centripetal force causes what is called a centripetal acceleration. The object accelerates in the direction of the center of the circle but, since it is also moving in a certain direction, it continually overshoots the center, which is why it moves in a circle (or ellipse). The centripetal acceleration depends on the square of the velocity of the object in the direction perpendicular to the line from the center of the circle to the object, the tangential velocity, and the radius of the circle. The centripetal force is the centripetal acceleration times the mass of the object.
ac = vt2/r
Centripetal Acceleration = (Tangential Velocity)2 / Radius
Fc = m ac
Fc = m v2/r
Example
2: Solution: F=[MFR × v]e−[MFR × v]0 We know the velocity of the exiting air and, since the hovercraft is moving sideways, the air on the intake side of the propeller is moving sideways to it, meaning that the component flowing directly into it is nearly zero. To get the mass flow rate, we simply multiply the volume flow rate by the density of the air. MFR = VFR × Density Now we can plug the values into the thrust equation. The mass flow rate on both sides of the propeller has to be the same, otherwise, the propeller would have to make air magically appear or vanish! F = (0.1204 kg/s [8.26×10−3 slugs/s]
× 95 m/s [311.7 ft/s]) − (0.1204 kg/s [8.26×10−3 slugs/s]
× 0 m/s [0 ft/s]) Now that we know the centripetal force, we can find the radius of the turn, since we already know the mass and tangential velocity. We just take the equation for the centripetal force and solve it for the radius, then put in our values (with appropriate unit conversions). Fc = m v2/r We’re ready now to find how long the hovercraft takes to turn from north to east. To do this, we convert the velocity to angular velocity by dividing it by the radius. Once we have this, we know that the angle it travels is the angular velocity multiplied by the time. We know the angle is 90°, which is equal to π/2 radians, and will have just found the angular velocity, so we can use those numbers to find the time. ω = vt/r Conclusion: The hovercraft would take 35.9 seconds to turn from north to south, and the radius of the turn would be 86.0 m [280 ft]. |
The more thrust air you can redirect, the faster the hovercraft will respond to directional changes. This is why hovercraft usually have at least 2 rudders. Some models may have a cascade of as many as perhaps 5 rudder blades to change the direction of nearly all the thrust air. To be effective at low speeds, rudders must also turn at least 60 degrees in each direction. Rudders are usually shaped like a symmetrical airfoil to minimize drag (air resistance) and to maintain smooth airflow as the angle increases in order to prevent the rudder blade from stalling.


Figure 13-4: Rudders in the Hovercraft
Images ©2005 DiscoverHover
Quiz Questions
| ©2005 World Hovercraft Organization All rights reserved. Copies of this Curriculum Guide may be printed for classroom use exclusively by DiscoverHover registered members. This Curriculum Guide and all materials contained in the DiscoverHover web site are protected by copyright laws and may not be reproduced, republished, distributed, or displayed on any other web site without the express prior written permission of the World Hovercraft Organization. |