DiscoverHover CURRICULUM GUIDE #5 - Experiment
© 2004 World Hovercraft Organization
PARTNER'S NAME
EXPERIMENT 5.1
Equipment:
1 600-mL or larger beaker (or 1-qt measuring cup or other large container)
1 100-mL graduated cylinder
water
two plastic or Styrofoam cups
handful of pennies
grease pencil
beam balance scale
aluminum foil
several large tubs or bowls
PART A: CALCULATING THE DENSITY OF A PENNY
- Weigh 10 pennies and record their mass on the data table. Divide this amount
by 10. This gives you the average mass of one penny. Record the mass on the
data table.
- Fill the graduated cylinder with 50 mL of water. Add the 10 pennies to the
water and notice that the water level rises. Subtract 50 mL from the new water
level shown. The remainder is the volume of water that the pennies displaced,
which is equal to the volume of the 10 pennies. Divide this volume by 10 to
give you the average volume of a single penny. Record these amounts on data
table 1.
- To find the average density of a penny, divide the mass of a penny by the
volume of a penny.
| ITEM |
10 PENNIES |
1 PENNY |
| |
|
|
| VOLUME |
|
|
| MASS |
|
|
| DENSITY |
|
|
PART B: MAKING PENNIES FLOAT
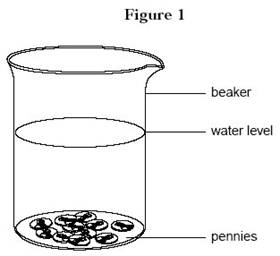
- Fill the container (large beaker, measuring cup, or bowl) halfway with water.
Mark the water level on the side of the container using the grease pencil.
In this and all following procedures, the accuracy of your markings is very
important.
-
Place all the pennies in the container. Mark this water
level on the container (see figure 1).
- Remove the pennies, weigh them, and record their mass on data table 2.
- Restore the water level to its original level if necessary.
- Weigh one of the plastic or Styrofoam cups, record its mass, and mark this
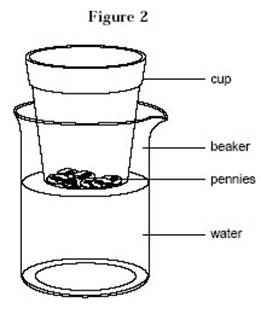
as “cup 1”. Place the cup on the water. Mark the new water level.
Be very accurate.
- Place all the pennies into the cup (see figure 2) and observe what happens.
Mark the new water level.
- Weigh the other cup, record its mass, and mark this as “cup 2”.
- While the cup with the pennies is still in the water, restore the water
level to what it was in step 4 by dipping or pouring water out of the container
into cup 2. Be careful not to spill any water. Remember, accuracy is extremely
important to the results of this experiment.
- Weigh cup 2 with the water in it, and record this mass.
- Remove cup 1 from the water, weigh it with the pennies in it, and record
its mass. Be careful not to lose any water from the container when you remove
the cup. Compare the masses of both cups.
- Place cup 2 with the water in it into the container so that it’s floating
on the water, and note the water level of the container.
| Weight of pennies |
|
| Weight of cup #1 |
|
| Weight of cup #2 |
|
| Weight of cup #1 with pennies |
|
| Weight of cup #2 with water |
|
- Archimedes’ principle states that in order for an object to float,
it must displace its weight in water. Did your results agree or disagree with
this statement? How?
- Why doesn’t a penny float? Think about what volume of water is necessary
to equal the weight of a penny and how that compares to the volume of the
penny.
- What would you have to do to float an object that is of higher density than
water?
- Why do the pennies in the cup float?
- Imagine that you have a tank full of water. Floating on the surface are
two buckets half full of rocks. Your job is to lower the water level in the
tank without removing anything from it. (All the water, buckets, and rocks
must remain in the tank). Explain how you can do this and why it will work.
WHAT’S GOING ON:
The results should agree. The floating cup with the pennies in it displaces
its weight in water. The pennies that sink displace their volume in water. A
penny does not float because it is more dense than water. Pennies are made of
zinc (density = 446 lb/ft3 [70060 N/m3]) and copper (density = 558 lb/ft3 [87650
N/m3]), two metals that have a greater density than water. Remember water’s
density is only 62.42 lb/ft3 [9806 N/m3]. To float an object more dense than
water, you would have to find some way of increasing its volume without increasing
its weight. By placing the pennies in the cup, a larger volume of water is displaced
than if just the pennies were dropped in the water. The combined density of
the cup, the pennies, and the air filling the cup is less than the water, so
the cup with the pennies in it floats.
Answer to #16: Move the rocks from one bucket into the other.
This will increase the weight of the second bucket enough that the buoyant force
can’t hold it above the water. As the second bucket sinks, water pours
into the bucket. The water that was displaced by the second bucket is now inside
the bucket, meaning the water level will drop.
RESULTS:
1 mL of water has a mass of 1 g. Since density = volume ÷ mass, the density
of water is 1 g/mL. Water’s density is used by scientists as the standard
of comparison against which all other densities are measured. If an object is
more dense than water, it sinks. If it is less dense, it floats. In either case,
it will displace some amount of water, since no two objects can occupy the same
space at the same time. In this experiment, you saw that floating and sinking
objects displace different amounts of water and how this is related to an object’s
density.
PART C: DESIGN YOUR OWN BOAT!
- Divide the class into groups of 2 or 3.
- Cut aluminum foil into square pieces about 6 in x 6 in. The exact size isn’t
important as long as each piece is the same size.
- Give each group a large tub or bowl full of water, one of the aluminum foil
pieces, and a handful of pennies.
- Try to shape your group’s foil into a boat that can hold as many pennies
as possible. Remember that the foil shape that displaces the largest volume
of water will hold the most pennies.
EXPERIMENT 5.2
Equipment:
- piece of aluminum with wire support
- a spring scale or pan scale
- a 1000 ml beaker full of water
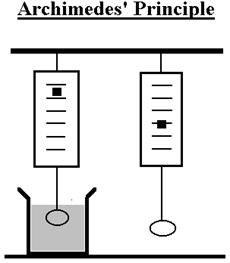
The purpose of this experiment is to demonstrate Archimedes' Law by calculating
the density of aluminum and then comparing the result with known textbook values.
- Attach the aluminum to the scale and measure the weight of the aluminum
both when hanging in air and when suspended in the water, as shown in the
figure.
- Calculate the difference in weight between air and water. Archimedes’
principle states that this difference in weight comes from the buoyant force
and is equal to the weight of the water displaced by the aluminum.
- Use the weight of the water (the difference in the two aluminum weights)
and the density of water to calculate the volume of the water displaced. Remember
that density is equal to weight divided by volume.
- We know that the volume of the water displaced is equal to the volume of
the aluminum, so we just need to measure the mass of the aluminum in order
to calculate the density.
- Look in a textbook to find the known density of aluminum. See if it compares
to your calculated value.